In deep studying, classification fashions don’t simply have to make predictions—they should specific confidence. That’s the place the Softmax activation perform is available in. Softmax takes the uncooked, unbounded scores produced by a neural community and transforms them right into a well-defined chance distribution, making it potential to interpret every output because the chance of a selected class.
This property makes Softmax a cornerstone of multi-class classification duties, from picture recognition to language modeling. On this article, we’ll construct an intuitive understanding of how Softmax works and why its implementation particulars matter greater than they first seem. Try the FULL CODES here.
Implementing Naive Softmax
import torch
def softmax_naive(logits):
exp_logits = torch.exp(logits)
return exp_logits / exp_logits.sum(dim=1, keepdim=True)This perform implements the Softmax activation in its most simple kind. It exponentiates every logit and normalizes it by the sum of all exponentiated values throughout lessons, producing a chance distribution for every enter pattern.
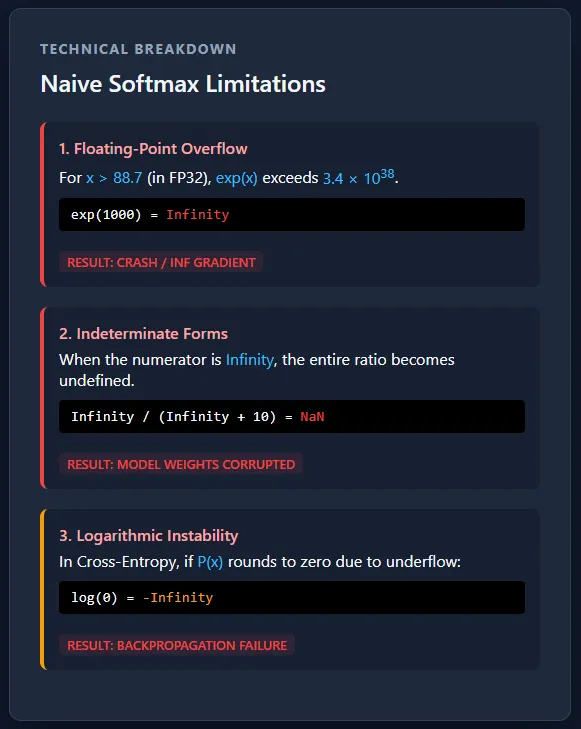
Whereas this implementation is mathematically right and simple to learn, it’s numerically unstable—giant optimistic logits could cause overflow, and huge adverse logits can underflow to zero. In consequence, this model must be averted in actual coaching pipelines. Try the FULL CODES here.
Pattern Logits and Goal Labels
This instance defines a small batch with three samples and three lessons as an example each regular and failure circumstances. The primary and third samples comprise cheap logit values and behave as anticipated throughout Softmax computation. The second pattern deliberately contains excessive values (1000 and -1000) to exhibit numerical instability—that is the place the naive Softmax implementation breaks down.
The targets tensor specifies the right class index for every pattern and might be used to compute the classification loss and observe how instability propagates throughout backpropagation. Try the FULL CODES here.
# Batch of three samples, 3 lessons
logits = torch.tensor([
[2.0, 1.0, 0.1],
[1000.0, 1.0, -1000.0],
[3.0, 2.0, 1.0]
], requires_grad=True)
targets = torch.tensor([0, 2, 1])Ahead Move: Softmax Output and the Failure Case
Through the ahead cross, the naive Softmax perform is utilized to the logits to supply class possibilities. For regular logit values (first and third samples), the output is a legitimate chance distribution the place values lie between 0 and 1 and sum to 1.
Nonetheless, the second pattern clearly exposes the numerical concern: exponentiating 1000 overflows to infinity, whereas -1000 underflows to zero. This leads to invalid operations throughout normalization, producing NaN values and nil possibilities. As soon as NaN seems at this stage, it contaminates all subsequent computations, making the mannequin unusable for coaching. Try the FULL CODES here.
# Ahead cross
probs = softmax_naive(logits)
print("Softmax possibilities:")
print(probs)Goal Chances and Loss Breakdown
Right here, we extract the expected chance akin to the true class for every pattern. Whereas the primary and third samples return legitimate possibilities, the second pattern’s goal chance is 0.0, brought on by numerical underflow within the Softmax computation. When the loss is calculated utilizing -log(p), taking the logarithm of 0.0 leads to +∞.
This makes the general loss infinite, which is a essential failure throughout coaching. As soon as the loss turns into infinite, gradient computation turns into unstable, resulting in NaNs throughout backpropagation and successfully halting studying. Try the FULL CODES here.
# Extract goal possibilities
target_probs = probs[torch.arange(len(targets)), targets]
print("nTarget possibilities:")
print(target_probs)
# Compute loss
loss = -torch.log(target_probs).imply()
print("nLoss:", loss)Backpropagation: Gradient Corruption
When backpropagation is triggered, the influence of the infinite loss turns into instantly seen. The gradients for the primary and third samples stay finite as a result of their Softmax outputs had been well-behaved. Nonetheless, the second pattern produces NaN gradients throughout all lessons as a result of log(0) operation within the loss.
These NaNs propagate backward by the community, contaminating weight updates and successfully breaking coaching. For this reason numerical instability on the Softmax–loss boundary is so harmful—as soon as NaNs seem, restoration is almost inconceivable with out restarting coaching. Try the FULL CODES here.
loss.backward()
print("nGradients:")
print(logits.grad)Numerical Instability and Its Penalties
Separating Softmax and cross-entropy creates a severe numerical stability threat because of exponential overflow and underflow. Massive logits can push possibilities to infinity or zero, inflicting log(0) and resulting in NaN gradients that shortly corrupt coaching. At manufacturing scale, this isn’t a uncommon edge case however a certainty—with out secure, fused implementations, giant multi-GPU coaching runs would fail unpredictably.
The core numerical downside comes from the truth that computer systems can’t characterize infinitely giant or infinitely small numbers. Floating-point codecs like FP32 have strict limits on how large or small a price will be saved. When Softmax computes exp(x), giant optimistic values develop so quick that they exceed the utmost representable quantity and switch into infinity, whereas giant adverse values shrink a lot that they change into zero. As soon as a price turns into infinity or zero, subsequent operations like division or logarithms break down and produce invalid outcomes. Try the FULL CODES here.
Implementing Steady Cross-Entropy Loss Utilizing LogSumExp
This implementation computes cross-entropy loss immediately from uncooked logits with out explicitly calculating Softmax possibilities. To keep up numerical stability, the logits are first shifted by subtracting the utmost worth per pattern, guaranteeing exponentials keep inside a secure vary.
The LogSumExp trick is then used to compute the normalization time period, after which the unique (unshifted) goal logit is subtracted to acquire the right loss. This method avoids overflow, underflow, and NaN gradients, and mirrors how cross-entropy is carried out in production-grade deep studying frameworks. Try the FULL CODES here.
def stable_cross_entropy(logits, targets):
# Discover max logit per pattern
max_logits, _ = torch.max(logits, dim=1, keepdim=True)
# Shift logits for numerical stability
shifted_logits = logits - max_logits
# Compute LogSumExp
log_sum_exp = torch.log(torch.sum(torch.exp(shifted_logits), dim=1)) + max_logits.squeeze(1)
# Compute loss utilizing ORIGINAL logits
loss = log_sum_exp - logits[torch.arange(len(targets)), targets]
return loss.imply()Steady Ahead and Backward Move
Operating the secure cross-entropy implementation on the identical excessive logits produces a finite loss and well-defined gradients. Though one pattern comprises very giant values (1000 and -1000), the LogSumExp formulation retains all intermediate computations in a secure numerical vary. In consequence, backpropagation completes efficiently with out producing NaNs, and every class receives a significant gradient sign.
This confirms that the instability seen earlier was not brought on by the information itself, however by the naive separation of Softmax and cross-entropy—a problem absolutely resolved through the use of a numerically secure, fused loss formulation. Try the FULL CODES here.
logits = torch.tensor([
[2.0, 1.0, 0.1],
[1000.0, 1.0, -1000.0],
[3.0, 2.0, 1.0]
], requires_grad=True)
targets = torch.tensor([0, 2, 1])
loss = stable_cross_entropy(logits, targets)
print("Steady loss:", loss)
loss.backward()
print("nGradients:")
print(logits.grad)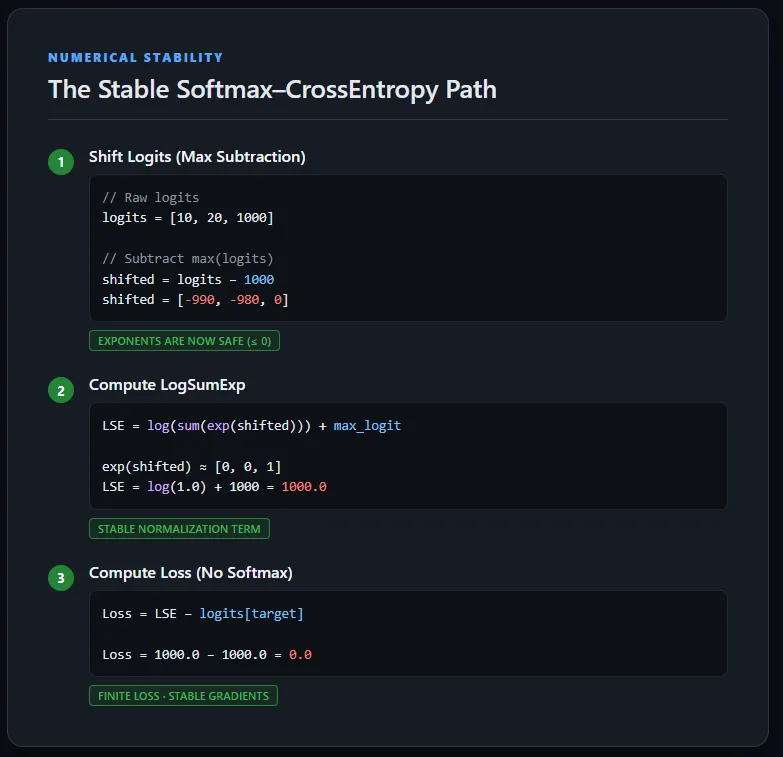

Conclusion
In follow, the hole between mathematical formulation and real-world code is the place many coaching failures originate. Whereas Softmax and cross-entropy are mathematically well-defined, their naive implementation ignores the finite precision limits of IEEE 754 {hardware}, making underflow and overflow inevitable.
The important thing repair is straightforward however essential: shift logits earlier than exponentiation and function within the log area every time potential. Most significantly, coaching not often requires specific possibilities—secure log-probabilities are adequate and much safer. When a loss immediately turns into NaN in manufacturing, it’s usually a sign that Softmax is being computed manually someplace it shouldn’t be.
Try the FULL CODES here. Additionally, be happy to observe us on Twitter and don’t neglect to hitch our 100k+ ML SubReddit and Subscribe to our Newsletter. Wait! are you on telegram? now you can join us on telegram as well.
Try our newest launch of ai2025.dev, a 2025-focused analytics platform that turns mannequin launches, benchmarks, and ecosystem exercise right into a structured dataset you possibly can filter, evaluate, and export

I’m a Civil Engineering Graduate (2022) from Jamia Millia Islamia, New Delhi, and I’ve a eager curiosity in Knowledge Science, particularly Neural Networks and their software in varied areas.

